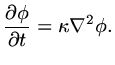Next: 1 Model Problem
Up: Numerical Computation Notes
Previous: Contents
Contents
Much impetus for the development of supercomputing facilities has been to
enable calculation of approximate solutions of PDE's, particularly those occuring
for large physical systems such as weather, flight or ship hydrodynamics.
It is important to realise that there are
different levels of approximation which lead to a physical prediction such as drag.
The real, physical situation has to be modelled mathematically and that will introduce
approximations such as two-dimensionality, semi-infinite domains and so on.
Next the resulting differential equations from the model need to be discretised
intoducing another set of approximations. Finally the discrete system needs to be
solved and again this is often only done approximately, either because physical constants
may be known only approximately or because the discrete system
has only an approximate numerical solution.
You need to be aware that `numerical algorithm' can be used in a number of different
contexts and is often used to
refer to discretisation of a continuous differential model and to refer to how you obtain
an approximate solution of a discrete system.
In describing the variation of physical quantities we use functions: displacement as a function of
time and so on. Thus it is important to think about how functions come about.
If we consider a simple example, 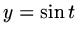 ,
then
,
then 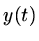 could equally well be defined by
could equally well be defined by
(a) geometrically by using a unit circle,
(b) algebraically by using a power series,
(c) as the solution of a differential equation
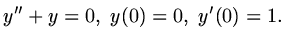 |
(1) |
Most of the functions we use in physics and engineering are defined only by the last method: they
are defined by a differential equation. Our experience is that most such equations
have to be solved numerically.
Another question which should occur to you is why do we have definitions of functions in terms of
differential equations in the first place?
The main reason is because in engineering and physics we are usually looking at functions which
are solutions of conservations laws;
laws which relate rates of change of quantities in space and time. Such laws usually fall into only a few
simple classes.
Conservation laws
(a) steady problem without sources: what comes into a region must leave.
So if
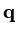 is the flux of some quantity
is the flux of some quantity 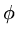 , in two dimensions,
, in two dimensions,
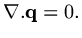 |
(2) |
If then there is a relation such as
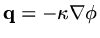 for a potential
(or temperature or ...) then
for a potential
(or temperature or ...) then
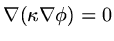 |
(3) |
or if 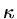 is constant,
is constant,
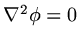 , a simple elliptic equation.
, a simple elliptic equation.
(b) unsteady problem: what comes into a volume either stays (and changes the amount in a volume) or leaves.
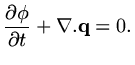 |
(4) |
So depending on the relation between the flux and the quantity 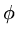 we get most of the simple PDE's which you have studied in your mathematics courses.
As an example, if the flux is determined by diffusion,
we get most of the simple PDE's which you have studied in your mathematics courses.
As an example, if the flux is determined by diffusion,
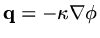 , then
, then
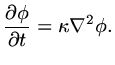 |
(5) |
Hence systems of partial differential equations can be just the mathematical expression
of conservation laws, and it is very common to end up with two space derivatives
(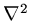 is the divergence of a gradient).
is the divergence of a gradient).
Our plan is to examine how simple differential systems can be discretised
(approximate solution of the discretised system will come in section 2) in a number
of ways, some of which reflect the physical basis of the equations. We do this
via a simple model
problem and a series of observations which extend the model problem to cover
many aspects of numerical solution of PDE's.
Subsections




Next: 1 Model Problem
Up: Numerical Computation Notes
Previous: Contents
Contents
Last changed 2000-11-21
![]() ,
then
,
then ![]() could equally well be defined by
could equally well be defined by
![]() is the flux of some quantity
is the flux of some quantity ![]() , in two dimensions,
, in two dimensions,
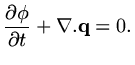
![]() we get most of the simple PDE's which you have studied in your mathematics courses.
As an example, if the flux is determined by diffusion,
we get most of the simple PDE's which you have studied in your mathematics courses.
As an example, if the flux is determined by diffusion,
![]() , then
, then