



Next: 4 Some General Theory
Up: 1 Introduction
Previous: 2 Gauss-Seidel iteration
Contents
Suppose a scalar 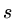 is determined by
is determined by 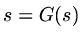 and we iterated
and we iterated
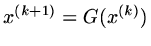 ,
then this could be written
,
then this could be written
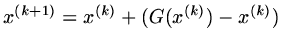 , or
, or
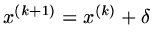 where
where
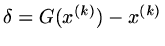 . In many situations,
over a number of iterations,
. In many situations,
over a number of iterations, 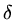 is consistently either too large or too small. So in some
situations, it is possible to accelerate convergence by taking a multiple of
is consistently either too large or too small. So in some
situations, it is possible to accelerate convergence by taking a multiple of 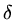 so that
so that
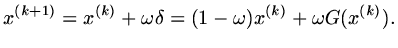 |
(139) |
This is the basis of relaxation; if 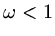 we speak of under-relaxation,
if
we speak of under-relaxation,
if 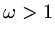 it is called over-relaxation.
If we apply this idea to Jacobi we would have
it is called over-relaxation.
If we apply this idea to Jacobi we would have
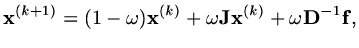 |
(140) |
so the iteration matrix would be
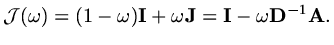 |
(141) |
It is more common to combine relaxation with a form of Gauss-Seidel. If we use
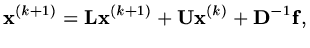 |
(142) |
to generate an increment 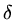 as in the scalar case, we will obtain
as in the scalar case, we will obtain
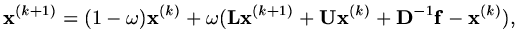 |
(143) |
so that
![$\displaystyle {\rm\bf x}^{(k+1)}=(I-\omega {\rm\bf L})^{-1}[(1-\omega ){\rm\bf I}+\omega{\rm\bf U}]{\rm\bf x}^{(k)},$](img359.png) |
(144) |
and the iteration matrix is
![$\displaystyle {\mathcal H}(\omega )=(I-\omega {\rm\bf L})^{-1}[(1-\omega ){\rm\bf I}+\omega{\rm\bf U}].$](img360.png) |
(145) |




Next: 4 Some General Theory
Up: 1 Introduction
Previous: 2 Gauss-Seidel iteration
Contents
Last changed 2000-11-21