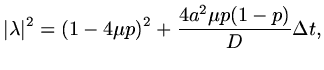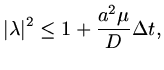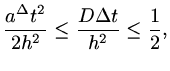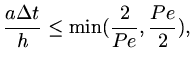Next: 2 Iterative Methods for
Up: 2 Stability
Previous: 2 Fourier Analysis of
Contents
We have assumed that the largest growth rate modulus must be bounded by 1
for stability; it is possible to conclude that there will be stability in
the sense that solutions
remain bounded, provided the largest eigenvalue of
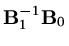 satisfies
satisfies
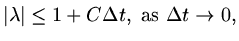 |
(117) |
for some constant 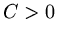 , since then
, since then
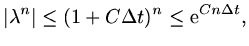 |
(118) |
and so
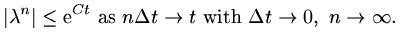 |
(119) |
This is called Lax-Richtmyer stability.
However for practical purposes, if the modulus of 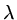 exceeds 1 for finite
exceeds 1 for finite
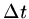 then the calculations invariably become too large to handle.
Hence it is safer to require practical or strict stability,
then the calculations invariably become too large to handle.
Hence it is safer to require practical or strict stability,
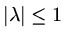 .
.
Example: Convection Diffusion
Consider an explicit discretisation of a convection-diffusion equation,
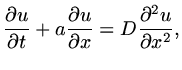 |
(120) |
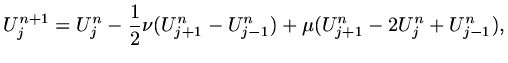 |
(121) |
where
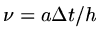 ,
,
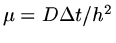 . Using a Fourier mode
. Using a Fourier mode
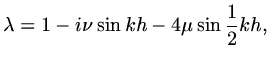 |
(122) |
so if
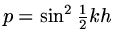 ,
,
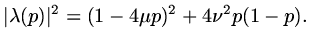 |
(123) |
(a) Lax-Richtmyer Stability
If we write
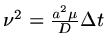 , then
, then
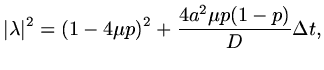 |
(124) |
and provided
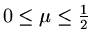 , we will have
, we will have
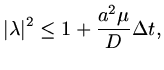 |
(125) |
so that the scheme will be L-R stable for
 with
with
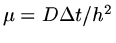 fixed. However in practice this is not sufficiently strong, for instance with
fixed. However in practice this is not sufficiently strong, for instance with
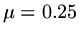 ,
,
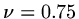 ,
,
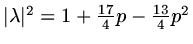 so that growth factors of greater than 1 occur for a range of small values of
so that growth factors of greater than 1 occur for a range of small values of
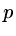 leading to breakdown of a calculation.
leading to breakdown of a calculation.
(b) Practical Stability
If we write
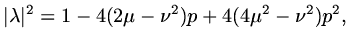 |
(126) |
then
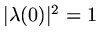 and
and
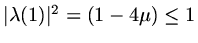 provided
provided
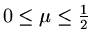 .
Since we are just dealing with a quadratic all we need have is the slope (with respect to
.
Since we are just dealing with a quadratic all we need have is the slope (with respect to 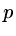 ) to negative at
) to negative at 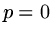 in order for
in order for
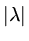 to be less than 1
over the range
to be less than 1
over the range
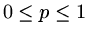 .
Hence we also need
.
Hence we also need
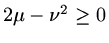 .
This can be rearranged as
.
This can be rearranged as
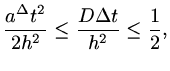 |
(127) |
or
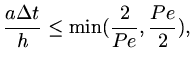 |
(128) |
where 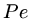 is the mesh Peclet number,
is the mesh Peclet number, 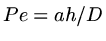 .
.




Next: 2 Iterative Methods for
Up: 2 Stability
Previous: 2 Fourier Analysis of
Contents
Last changed 2000-11-21
![]() satisfies
satisfies
![]() exceeds 1 for finite
exceeds 1 for finite
![]() then the calculations invariably become too large to handle.
Hence it is safer to require practical or strict stability,
then the calculations invariably become too large to handle.
Hence it is safer to require practical or strict stability,
![]() .
.
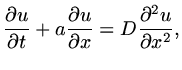
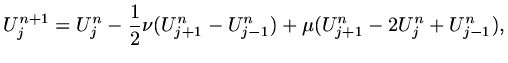
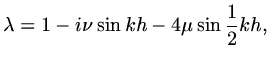
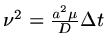 , then
, then