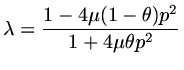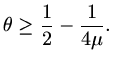Next: 3 Practical Stability
Up: 2 Stability
Previous: 1 Introduction
Contents
It can be very difficult to calculate all of the eigenvalues of the iteration matrix.
One approach which has been very successful in provinding practical stability
criteria is to extend the domain of the PDE to the whole real line (or the
whole plane ...) and then to look at stability of Fourier modes. On the real line, if
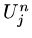 is assumed to behave like
is assumed to behave like
![$\displaystyle U^n_j\sim [\lambda(k)]^n{\rm e}^{ikjh},$](img268.png) |
(104) |
(a discrete analogue of
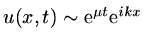 )
then we can examine
)
then we can examine
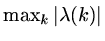 to decide on stability of the
numerical scheme. It is important to realise that although practical problems do not
have infinite domains, they do not have constant coefficients; nevertheless criteria which
have come from Fourier analysis of model problems are usually very good predictors
for the behaviour of a numerical scheme.
to decide on stability of the
numerical scheme. It is important to realise that although practical problems do not
have infinite domains, they do not have constant coefficients; nevertheless criteria which
have come from Fourier analysis of model problems are usually very good predictors
for the behaviour of a numerical scheme.
Example 1: Heat Equation
If we have
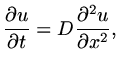 |
(105) |
and we discretise explicitly,
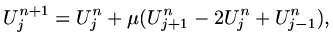 |
(106) |
where
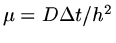 , then substituting the Fourier mode gives
, then substituting the Fourier mode gives
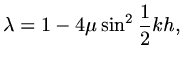 |
(107) |
so that 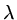 is real and
is real and
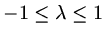 provided
provided
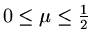 .
This is a very stringent criterion, equivalent to
.
This is a very stringent criterion, equivalent to
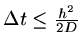 . If the mesh is refined
then the time step has to be reduced by a factor equal to the square of the refinement.
. If the mesh is refined
then the time step has to be reduced by a factor equal to the square of the refinement.
Example 2: Lax-Wendroff applied to a hyperbolic equation
One important method to generate a finite difference scheme is Lax-Wendroff whereby
the time derivatives in a Taylor expansion of
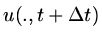 about
about 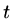 are replaced
by space derivatives using the differential equation, and those space derivatives
discretised using finite differences. We consider the model equation
are replaced
by space derivatives using the differential equation, and those space derivatives
discretised using finite differences. We consider the model equation
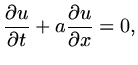 |
(108) |
where 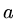 is constant. Since
is constant. Since
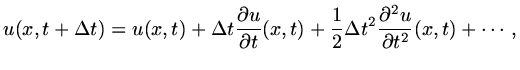 |
(109) |
and using 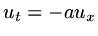 ,
,
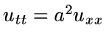 ,
,
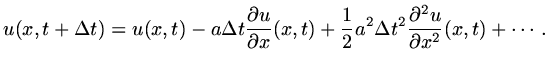 |
(110) |
This series is truncated after the third term to give a second order accurate scheme,
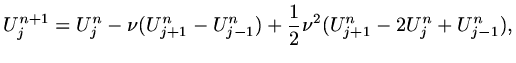 |
(111) |
where
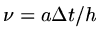 .
Substituting a Fourier mode gives,
.
Substituting a Fourier mode gives,
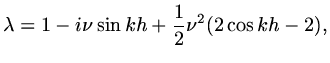 |
(112) |
so that 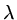 is complex. If
is complex. If
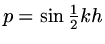 ,
,
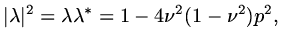 |
(113) |
and we will have
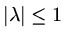 provided
provided
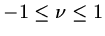 .
.
Example 3: 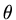 -method for Diffusion Equation
-method for Diffusion Equation
If we apply a 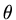 -method to a diffusion equation, then
-method to a diffusion equation, then
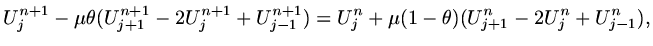 |
(114) |
where again
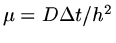 .
Substituting in a Fourier mode,
.
Substituting in a Fourier mode,
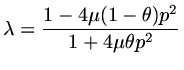 |
(115) |
with
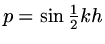 . We deduce that
. We deduce that
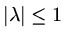 provided
provided
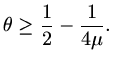 |
(116) |




Next: 3 Practical Stability
Up: 2 Stability
Previous: 1 Introduction
Contents
Last changed 2000-11-21
![]() is assumed to behave like
is assumed to behave like
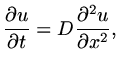
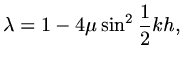
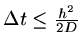 . If the mesh is refined
then the time step has to be reduced by a factor equal to the square of the refinement.
. If the mesh is refined
then the time step has to be reduced by a factor equal to the square of the refinement.
![]() about
about ![]() are replaced
by space derivatives using the differential equation, and those space derivatives
discretised using finite differences. We consider the model equation
are replaced
by space derivatives using the differential equation, and those space derivatives
discretised using finite differences. We consider the model equation
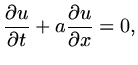
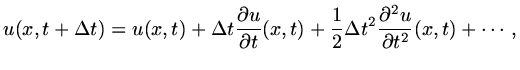
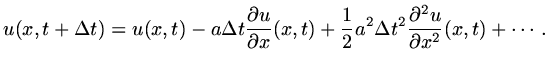
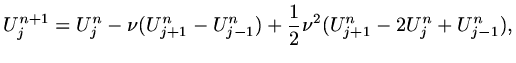
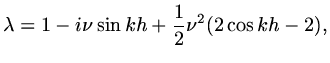
![]() -method for Diffusion Equation
-method for Diffusion Equation
![]() -method to a diffusion equation, then
-method to a diffusion equation, then