



Next: 2 Fourier Analysis of
Up: 2 Stability
Previous: 2 Stability
Contents
We have seen that time dependent problems are approximated by a vector of values,
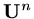 at each time step and further the form of the iteration for these values was
at each time step and further the form of the iteration for these values was
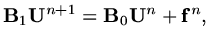 |
(96) |
where
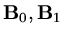 are matrices. If
are matrices. If
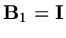 we called the method explicit, otherwise
we referred to an implicit method. If the PDE involved two or more space dimensions, it can
still be dealt with under this framework, elements of vector
we called the method explicit, otherwise
we referred to an implicit method. If the PDE involved two or more space dimensions, it can
still be dealt with under this framework, elements of vector
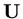 have just a more
complicated mapping onto the physical mesh. Thus in principle we have iterations of the
form
have just a more
complicated mapping onto the physical mesh. Thus in principle we have iterations of the
form
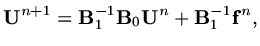 |
(97) |
to calculate the approximation time step by time step. Thus we need first to understand
some things about iterated sequences.
Suppose we have the sequence
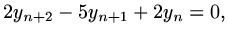 |
(98) |
with 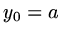 ,
, 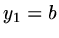 .
We look for a solution
.
We look for a solution
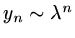 so that
so that
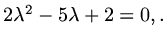 The roots are
The roots are
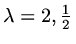 and the general solution
is
and the general solution
is
 . Using the initial conditions
. Using the initial conditions
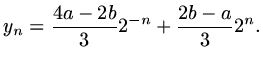 |
(99) |
Now suppose we choose the inital values 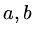 such that
such that 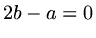 , then
, then
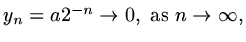 and it might appear that we have a sensible computation to determine
and it might appear that we have a sensible computation to determine 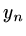 .
However suppose, because of finite machine accuracy, that
.
However suppose, because of finite machine accuracy, that
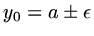 ,
,
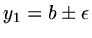 ,
then
,
then
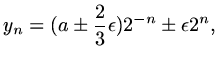 |
(100) |
and for example, if
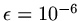 (typical single precison accuracy)
then
(typical single precison accuracy)
then
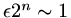 after only
after only 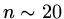 iterations! Hence we could not
carry out any practical computations using this iteration without the calulations
being swamped by the growing solution even though the `solution' should have no
component of this mode.
iterations! Hence we could not
carry out any practical computations using this iteration without the calulations
being swamped by the growing solution even though the `solution' should have no
component of this mode.
Consider now a matrix example,
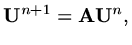 |
(101) |
where
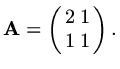 |
(102) |
We look for a solution where
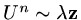 so that
so that
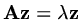 , and
, and 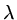 is an eigenvalue of
the iteration matrix
is an eigenvalue of
the iteration matrix
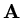 . In this case the eigenvalues are
. In this case the eigenvalues are
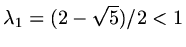 ,
,
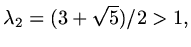 and if we denote
the eigenvectors by
and if we denote
the eigenvectors by
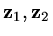 , the general solution is
, the general solution is
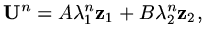 |
(103) |
where 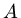 and
and 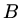 are constants. Again, if we choose the inital data so that
are constants. Again, if we choose the inital data so that
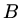 is zero, machine rounding errors
will still produce a growing component which will swamp the calculation very quickly.
is zero, machine rounding errors
will still produce a growing component which will swamp the calculation very quickly.
Thus one difficulty with calculating iterated sequences is that growing modes lead to
rapid breakdown of a calculation and this `instability' may not be a part of the
original
physical system, but introduced as an artefact of the discretisation of the continuous
system. Often stability is a more challenging practical problem than accuracy.
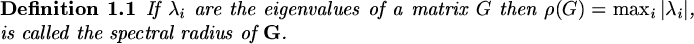
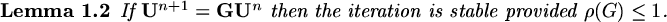




Next: 2 Fourier Analysis of
Up: 2 Stability
Previous: 2 Stability
Contents
Last changed 2000-11-21
![]() at each time step and further the form of the iteration for these values was
at each time step and further the form of the iteration for these values was
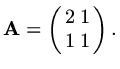
![]()
![]()