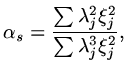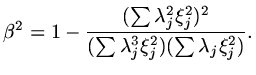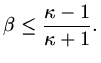Next: 2 Conjugate Gradient Algorithm
Up: 2 Conjugate Gradient Iteration
Previous: 2 Conjugate Gradient Iteration
Contents
Suppose
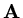 is a real symmetric positive definite matrix (so that
is a real symmetric positive definite matrix (so that
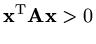 for all non-zero
for all non-zero
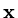 ) and consider the function
) and consider the function
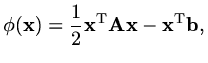 |
(170) |
then
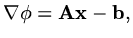 |
(171) |
so that 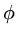 will be a minimum when
will be a minimum when
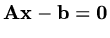 . So to solve the matrix equation
. So to solve the matrix equation
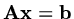 we can try to find a minimum of the function
we can try to find a minimum of the function 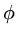 . We can use this idea to generate an
iterative method to determine an approximate solution of the original matrix equation.
. We can use this idea to generate an
iterative method to determine an approximate solution of the original matrix equation.
If we have an approximation
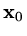 then the residual,
then the residual,
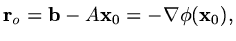 |
(172) |
will give the direction of fastest descent from the curve
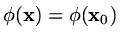 at the point
at the point
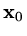 .
So we can find a value
.
So we can find a value
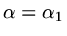 for which
for which
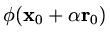 is smallest.
If we solve
is smallest.
If we solve
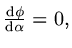 we obtain
we obtain
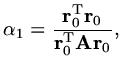 |
(173) |
so that an iteration algorithm is:
Steepest descents
Choose an initial guess
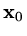 (e.g.
(e.g.
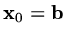 ), tolerance
), tolerance 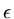 and calculate
and calculate
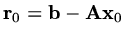 ,
in
loop for
,
in
loop for
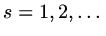
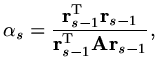
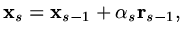
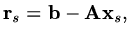 until
until
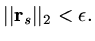
This algorithm can converge slowly because it may be repetitively calculating
the same few search directions with only small changes of components in other directions.
Convergence
If the true solution is
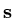 and the error is
and the error is
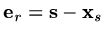 , the iteration formula gives
, the iteration formula gives
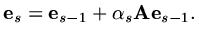 |
(174) |
If the eigenvalues and eigenvectors of
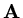 are
are 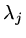 ,
,
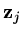 and the error
is written in terms of
and the error
is written in terms of
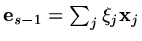 (for some numbers
(for some numbers 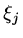 ,
leaving out the
,
leaving out the 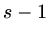 index),
algebra gives
index),
algebra gives
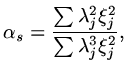 |
(175) |
and we can find the error at the next step. Using a norm
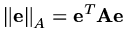 ,
,
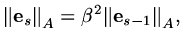 |
(176) |
where
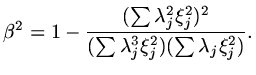 |
(177) |
This formula is not much use without knowing the values of 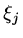 but we can ask
what is the
largest value it can have over all possible combinations of
but we can ask
what is the
largest value it can have over all possible combinations of 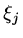 . The method to
answer this question is beyond
this course, but if the condition number of the matrix
. The method to
answer this question is beyond
this course, but if the condition number of the matrix
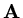 is
is 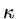 then
then
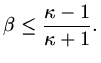 |
(178) |
So convergence becomes slower as the condition number increases but is good if
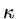 is less than around 10.
is less than around 10.




Next: 2 Conjugate Gradient Algorithm
Up: 2 Conjugate Gradient Iteration
Previous: 2 Conjugate Gradient Iteration
Contents
Last changed 2000-11-21
![]() is a real symmetric positive definite matrix (so that
is a real symmetric positive definite matrix (so that
![]() for all non-zero
for all non-zero
![]() ) and consider the function
) and consider the function
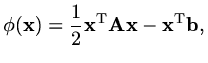
![]() then the residual,
then the residual,
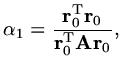
![]() (e.g.
(e.g.
![]() ), tolerance
), tolerance ![]() and calculate
and calculate
![]() ,
in
loop for
,
in
loop for
![]()
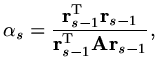
![]()
![]() until
until
![]()
![]() and the error is
and the error is
![]() , the iteration formula gives
, the iteration formula gives