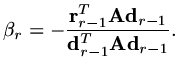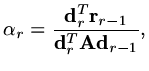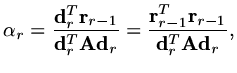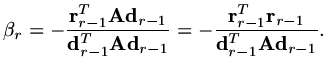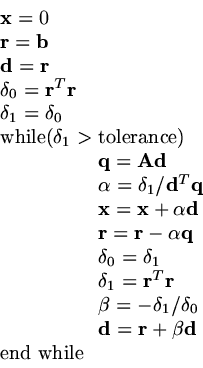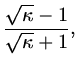Next: 3 Multigrid Iteration
Up: 2 Conjugate Gradient Iteration
Previous: 1 Minimisation Problem &
Contents
We will call two vectors
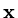 and
and
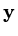 A-conjugate if
A-conjugate if
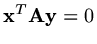 .
We can also see that if we denote the characteristic polynomial of
.
We can also see that if we denote the characteristic polynomial of
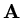 as
as
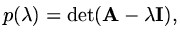 |
(179) |
then Cayley-Hamilton's theorem tells us that
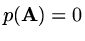 too. If we suppose
too. If we suppose
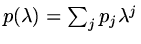 , then
, then
 |
(180) |
and so, as the matrix is non-singular (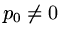 ),
),
![$\displaystyle {\rm\bf A}^{-1}=-{1\over p_0}[p_1{\rm\bf I}+p_2{\rm\bf A}+\cdots +p_n{\rm\bf A}^{n-1}]$](img471.png) |
(181) |
and the solution
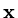 must be
must be
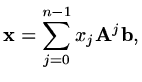 |
(182) |
where
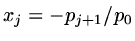 . Thus the solution is able to be expressed as a linear
combination of vectors of the form
. Thus the solution is able to be expressed as a linear
combination of vectors of the form
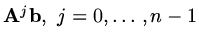 . Let
. Let
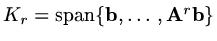 then one approximation strategy
is to try to find approximations from the subspaces
then one approximation strategy
is to try to find approximations from the subspaces
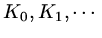 which successively minimise
which successively minimise 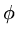 . After
. After 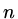 steps we must have
the solution but of course we hope that when
steps we must have
the solution but of course we hope that when 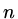 is very large,
we might obtain a good approximation after only a small number of steps.
The obvious way to do this
would be at step
is very large,
we might obtain a good approximation after only a small number of steps.
The obvious way to do this
would be at step 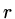 , approximating from
, approximating from 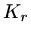 to try to find coefficients
to try to find coefficients 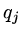 such
that if
such
that if
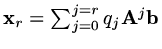 then
then
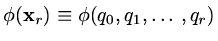 is minimised. In this case
is minimised. In this case
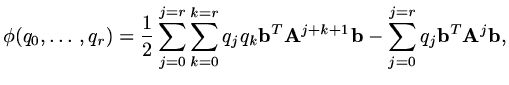 |
(183) |
and so setting the derivatives of 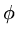 with respect to
with respect to
 to be zero
would mean solving another matrix system of growing size at each iteration.
The idea of conjugate gradient is to find coefficients only once in an expansion
of the solution in terms of a growing set of basis vectors. To do this we need a
different basis for
to be zero
would mean solving another matrix system of growing size at each iteration.
The idea of conjugate gradient is to find coefficients only once in an expansion
of the solution in terms of a growing set of basis vectors. To do this we need a
different basis for  . Suppose we call this basis
. Suppose we call this basis
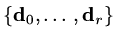 and that the basis vectors are
and that the basis vectors are 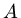 -conjugate.
Now if we let
-conjugate.
Now if we let
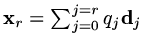 then
then
![$\displaystyle \phi (q_0,\ldots ,q_r)=\sum_{j=0}^{j=r}[{1\over 2}q_j^2{\rm\bf d}_j^{T}{\rm\bf A}{\rm\bf d}_j - q_j{\rm\bf d}_j^{T}{\rm\bf b}],$](img486.png) |
(184) |
so now the minimisation problem is almost trivial, each component 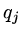 is independent
of the others and at each step, the existing components do not change. So we only
calculate the components in each direction once.
Of course we do have to construct the basis
is independent
of the others and at each step, the existing components do not change. So we only
calculate the components in each direction once.
Of course we do have to construct the basis
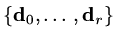 but since it
has to span
but since it
has to span 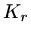 and at the
and at the 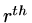 step we already have an
step we already have an 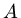 -conjugate basis for
-conjugate basis for 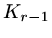 ,
all we have to do is compute one additional basis vector at each step.
,
all we have to do is compute one additional basis vector at each step.
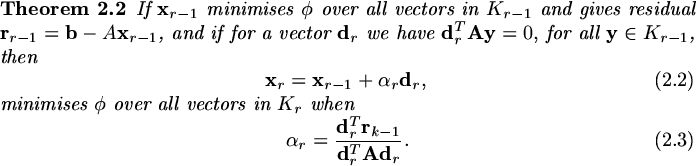
The proof is straight forward. It is almost trivial from our discussion above
that
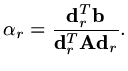 |
(185) |
Now
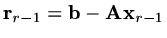 , so that
, so that
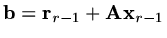 and as
and as
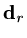 is A-conjugate with all vectors in
is A-conjugate with all vectors in 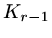 , including
, including
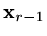 , we must have
, we must have
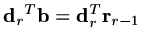 .
.
This enables us to carry out one iteration of the Conjugate Gradient algorithm.
Suppose
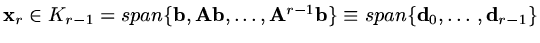 ,
minimises
,
minimises  over
over  and the basis vectors
and the basis vectors
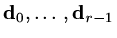 are
are
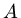 -conjugate. Calculate
-conjugate. Calculate
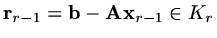 and suppose
and suppose
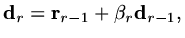 |
(186) |
where 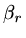 is chosen to make
is chosen to make
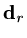
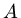 -conjugate to
-conjugate to
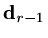 ,
,
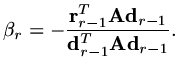 |
(187) |
If
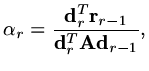 |
(188) |
is a search length, then
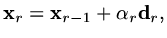 |
(189) |
minimises 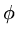 over
over 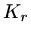 and
and
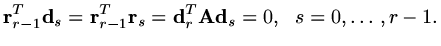 |
(190) |
Note that we can also show the
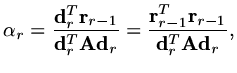 |
(191) |
and
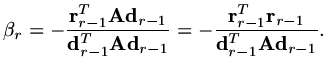 |
(192) |
It is worth observing that we only ever need to store four vectors,
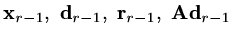 each of which can be replaced as the iteration
proceeds and other than the vector,
each of which can be replaced as the iteration
proceeds and other than the vector,
 there are only inner products to evaluate.
The algorthm is very compact,
there are only inner products to evaluate.
The algorthm is very compact,
Algorithm
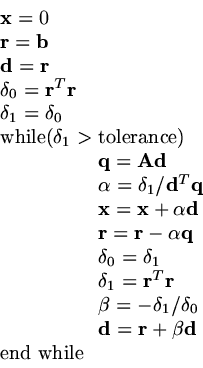 |
(193) |
We do not have time to develop an error analysis but we can note that if the condition
number of the matrix
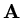 is
is 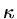 , then the error changes by a factor smaller or
equal to
, then the error changes by a factor smaller or
equal to
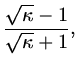 |
(194) |
each iteration. This is considerable better than for steepest descents. Even further
advantage can be gained by preconditioning the matrix
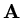 by pre-multiplying the equation
by pre-multiplying the equation
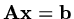 by an additional matrix. We shall not consider that aspect in this course.
by an additional matrix. We shall not consider that aspect in this course.




Next: 3 Multigrid Iteration
Up: 2 Conjugate Gradient Iteration
Previous: 1 Minimisation Problem &
Contents
Last changed 2000-11-21
![]() and
and
![]() A-conjugate if
A-conjugate if
![]() .
We can also see that if we denote the characteristic polynomial of
.
We can also see that if we denote the characteristic polynomial of
![]() as
as
![$\displaystyle {\rm\bf A}^{-1}=-{1\over p_0}[p_1{\rm\bf I}+p_2{\rm\bf A}+\cdots +p_n{\rm\bf A}^{n-1}]$](img471.png)
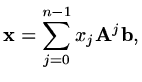
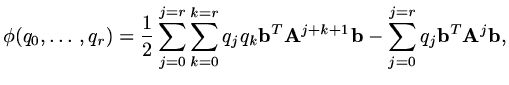
![$\displaystyle \phi (q_0,\ldots ,q_r)=\sum_{j=0}^{j=r}[{1\over 2}q_j^2{\rm\bf d}_j^{T}{\rm\bf A}{\rm\bf d}_j - q_j{\rm\bf d}_j^{T}{\rm\bf b}],$](img486.png)
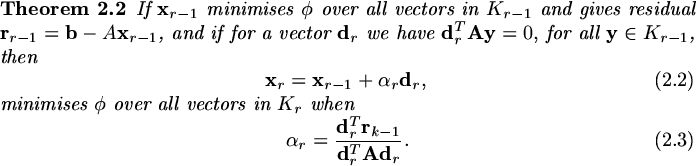
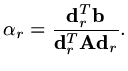
![]() ,
minimises
,
minimises ![]() over
over ![]() and the basis vectors
and the basis vectors
![]() are
are
![]() -conjugate. Calculate
-conjugate. Calculate
![]() and suppose
and suppose