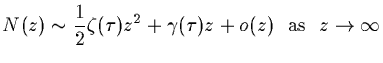1. Problems
(i) Riley(1987) gives one way of computing a Prandtl-Batchelor flow which might be applied to a channel flow if one assumes that there is potential flow through the channel with vorticity being confined to finite regions on the walls. If the channel has a symmetric expansion is it possible to compute an asymmetric Prandtl-Batchelor flow or are all solutions necessarily symmetric? Is it possible to compute asymmetric exterior Prandtl-Batchelor flows where the geometry and upstream outer flow is symmetric?
(ii) Can the
![]() theory be applied in a symmetric channel in the same way
as the
theory be applied in a symmetric channel in the same way
as the
![]() theory was applied by Borgas & Pedley; that is, as the limit
of an asymmetric channel becoming symmetric? My experience with computed solutions of
the two coupled non-linear boundary layer equations in a symmetric geometry is that when
they do converge, they converge to a symmetric solution. Is it possible to compute asymmetric solutions
by starting from an asymmetric initial condition or by introducing some form of psuedo time marching,
for instance by solving
theory was applied by Borgas & Pedley; that is, as the limit
of an asymmetric channel becoming symmetric? My experience with computed solutions of
the two coupled non-linear boundary layer equations in a symmetric geometry is that when
they do converge, they converge to a symmetric solution. Is it possible to compute asymmetric solutions
by starting from an asymmetric initial condition or by introducing some form of psuedo time marching,
for instance by solving
| (1) |
2. Software
(i) bpgen.f
generate solutions to Borgas & Pedley's variant of the
Falkner-Skan equation (10.17)
(ii) channel.f
time marching solution of Navier-Stokes equations for flow
thorough a sudden channel expansion using a rectangular grid. Time stepping of vorticity can
be by central, upwind, Lax-Wendroff or Quickest algorithms. Stream function-vorticity equation
solved using multigrid. You will need header file step.h
3. Corrections
(1) Equation (10.19) is missing a ![]() multiplying
multiplying
![]()