Chapter 3 & 4 - Triple deck

Material for both chapter 3 and chapter 4 is included in this one page.

1. Problems

(i) The transformation used by Dennis & Dunwoody(1966) has the attractive property that the leading and trailing edge points would not appear in a finite difference formulation. Does such a scheme provide enough accuracy to resolve the asymptotic structure of the drag coefficient? The computational domain has one less boundary than that used by McLachlan(1991) and if a potential solution was used for $\xi >\xi_{M-1}$ to relate stream-function values on the boundary, $\psi_{M,j}$, to the values $\psi_{M-1,k},\ k=0,\cdots, N$ as advocated by Fornberg, can this method be even more able to resolve fine second and third order variation in the drag coefficient than the computations of McLachlan? McLachlan had some trouble with mesh refinement near the trailing edge, with this transformation refinement at both the leading and trailing edge should be straightforward.

(ii) The potential flow region for flow about a plate seems to revolve around a number of loose ends. Suppose the plate is located on $0\le x\le 1, y=0$. Over the main body of the plate the outer potential should be like

$$w\sim z-{\rm i}\beta_0\sqrt{{2\over R}}z^{1/2},$$

the triple deck introduces a correction to this but not of order $z^{1/2}$, rather of order $(z-1)^{1/3}$ so far downstream the potential flow is still describing a body of parabolic extent rather than one where the flow returns to uniform velocity over the whole wake. Could this be rectified by assuming a distribution of sources $m(x,R)$ over $0\le x\le 1$ where $m$ was then expanded as an asymptotic sequence for large $R$? Obviously from continuity the sources would have to become sinks towards the trailing edge.

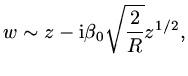
(iii) Talke & Berger(1970) used parabolic coordinates centred on the trailing edge to find a series truncation solution near the trailing edge using Goldstein's solution for the wake as an outer boundary condition. How would their results be modified if a series truncation solution near the trailing edge (in other words in a region of order $R^{-3/4}\times R^{-3/4}$) was matched to the near field triple deck solution rather than Goldstein's near wake? See also Berger & Scalise(1995)

2. Software

(i) newton.f program to solve trailing edge triple deck problem. The program requires a matrix inversion routine such as might be obtained from Numerical Recipies.
(ii) tdeck.m contour streamlines from output of triple deck program newton.f

Return to Contents page