1. Problems
(i) Batchelor conjectured that the correct limit for the Nav
ier-Stokes equations as
![]() and then
and then
![]() of a recirculation region is a constant vorticity
region of finite extent. Normally computations are based around letting
of a recirculation region is a constant vorticity
region of finite extent. Normally computations are based around letting
![]() to obtain a steady
solution and then allowing the Reynolds number to increase. Is it possible to compute solutions with the li
mits
interchanged, so
to obtain a steady
solution and then allowing the Reynolds number to increase. Is it possible to compute solutions with the li
mits
interchanged, so
![]() and then
and then
![]() ? One way this might be approached
would be to take a viscous calculation at finite Reynolds number as the starting point
for a time dependent inviscid (but rotational) calculation. How would a flow with a distribution
of vorticity from a viscous calculation subsequently develop if viscosity were suddenly switched off?
That is, from an initial distribution of vorticity
? One way this might be approached
would be to take a viscous calculation at finite Reynolds number as the starting point
for a time dependent inviscid (but rotational) calculation. How would a flow with a distribution
of vorticity from a viscous calculation subsequently develop if viscosity were suddenly switched off?
That is, from an initial distribution of vorticity
![]() and corresponding stream
function
and corresponding stream
function
![]() solve
solve
| (1) |
(ii) In Brown & Stewartson(1969) it is claimed that
logarithmic terms cancel so that the ![]() velocity is finite
on the separation line (page 57 of their paper).
It is very unusual for these normally meticulous authors not to reference
a detailed justification of a remark such as this. Can you either track down a
suitable reference or show this result yourself?
velocity is finite
on the separation line (page 57 of their paper).
It is very unusual for these normally meticulous authors not to reference
a detailed justification of a remark such as this. Can you either track down a
suitable reference or show this result yourself?
(iii) Modify Leigh's method using the initial profile
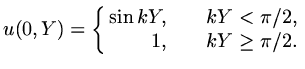 |
(2) |
| (3) |
(iv) Leigh and Terrill each use a semi-implicit method to solve a set of non-linear equations. Apply Newton's method to solve Terrill's discrete non-linear equations. Is the computation more efficient?
(v) Implement Kawaguti's method to solve the Navier-Stokes equations. In Kawaguti & Jain the
outer
boundary condition was relaxed to have just the stream-function and vorticity zero. What effect does
this have on the computed solution at ![]() ?
?
2. Software
(i) solvebrod.m
calculate first ![]() Brodetsky coefficients
Brodetsky coefficients
![]() for
given separation angle
for
given separation angle
(ii) brodgen.f
calculate flow using Brodetsky coefficients calculated by solvebrod.m
(iii) lcwcyl.f
Woods' method for cylinder with constant pressure on free streamline
(iv) lcwcyl2.f
Woods' extended model for cylinder with variable pressure on free streamline
(v) pohlhausen.f
Pohlhausen's method to solve integral form of boundary layer equation
with either Heimenz observations, potential flow or linear variation for flow at the boundary layer edge
(vi) fskan.f
determine existence of Falkner-Skan solutions by varying ![]() for fixed
for fixed ![]()
(vii) fskan1.f
determine existence of Falkner-Skan solutions by varying ![]() for fixed
for fixed
![]()
(viii) burgers.f
Burgers' method for either Heimenz or potential outer flow
(ix) leigh.f
Leigh's method for calculating solution of boundary layer equation
(x) terrill.f
Terrill's method for calculating solution of boundary layer equation
(xi) thom.f
Thom's method to calculate solution of Navier-Stokes equations for
flow about a cylinder