



Next: 5 Application to a
Up: 1 Introduction
Previous: 3 Relaxation
Contents
The reason we have taken so much effort to determine the iteration matrix is
that if
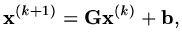 |
(146) |
and as the true solution
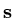 satisfies
satisfies
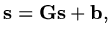 |
(147) |
so defining an error
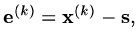 we must have
we must have
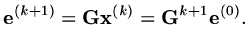 |
(148) |
Thus the iteration will converge provided
 tends to the zero matrix as
tends to the zero matrix as 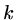 becomes
large.
becomes
large.
Theorem If
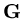 has eigenvalues
has eigenvalues 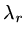 , the iteration converges
as
, the iteration converges
as
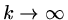 provided
provided
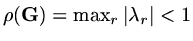 .
We call
.
We call 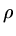 the spectral radius of the matrix
the spectral radius of the matrix
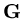 .
.
We consider only a special case, where there is a full set of eigenvalues, and if
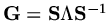 where
where 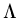 is a diagonal matrix of the eigenvalues,
then
is a diagonal matrix of the eigenvalues,
then
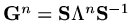 and this will become the zero vector provided the moduli
of all the eignevalues are less than one.
and this will become the zero vector provided the moduli
of all the eignevalues are less than one.
Theorem (Gershgorin) The eigenvalues of
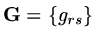 lie within the union of the discs
lie within the union of the discs
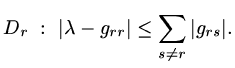 |
(149) |
This can be seen by supposing eigenvalue 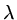 has eigenvector
has eigenvector
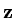 so that
so that
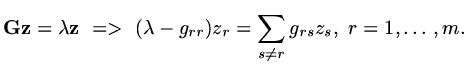 |
(150) |
Choose 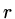 such that
such that
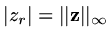 ,
and then
,
and then
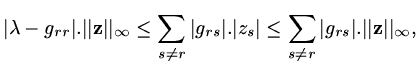 |
(151) |
whence the result follows.
Lemma Jacobi iteration will converge if
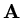 is strictly diagonally dominant,
is strictly diagonally dominant,
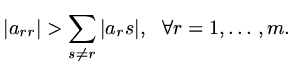 |
(152) |
In this case, using Jacobi iteration
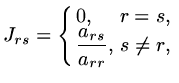 |
(153) |
so that for all eigenvalues of the iteration matrix,
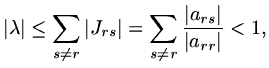 |
(154) |
so that all the eigenvalues of the iteration matrix must have moduli less than one.
Lemma Relaxation can converge only if
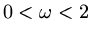 .
.
To show this, consider the eigenvalues of the iteration matrix,
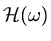 ,
,
![$\displaystyle [(1-\omega ){\rm\bf I}+\omega {\rm\bf U}]{\rm\bf z}=\lambda ({\rm\bf I}-\omega {\rm\bf L}){\rm\bf z},$](img388.png) |
(155) |
so that
![$\displaystyle [(1-\omega -\lambda ){\rm\bf I}+\omega{\rm\bf U}+\lambda\omega{\rm\bf L}]{\rm\bf z}=0.$](img389.png) |
(156) |
If we take the determinant of the coefficient matrix and look at the term which
is independent of 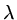 (and so is the product of all the eigenvalues), it is
(and so is the product of all the eigenvalues), it is
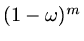 , so that if
, so that if
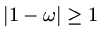 then at least one
eigenvalue must be greater than or equal to 1. Hence it is necessary that
then at least one
eigenvalue must be greater than or equal to 1. Hence it is necessary that
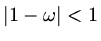 ,
or
,
or
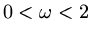 .
.
We do not have time to go into the mathematics deeply, but there will be a critical
value 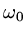 for which
for which
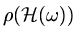 is a minimum. For most practical
matrices this optimum value of the relaxation parameter can be found from numerical
experiments.
is a minimum. For most practical
matrices this optimum value of the relaxation parameter can be found from numerical
experiments.




Next: 5 Application to a
Up: 1 Introduction
Previous: 3 Relaxation
Contents
Last changed 2000-11-21
![]() has eigenvalues
has eigenvalues ![]() , the iteration converges
as
, the iteration converges
as
![]() provided
provided
![]() .
We call
.
We call ![]() the spectral radius of the matrix
the spectral radius of the matrix
![]() .
.
![]() where
where ![]() is a diagonal matrix of the eigenvalues,
then
is a diagonal matrix of the eigenvalues,
then
![]() and this will become the zero vector provided the moduli
of all the eignevalues are less than one.
and this will become the zero vector provided the moduli
of all the eignevalues are less than one.
![]() lie within the union of the discs
lie within the union of the discs
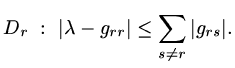
![]() has eigenvector
has eigenvector
![]() so that
so that
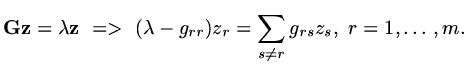
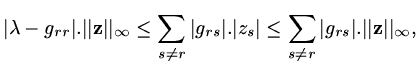
![]() is strictly diagonally dominant,
is strictly diagonally dominant,
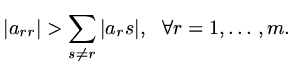
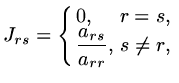
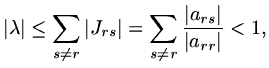
![]() .
.
![]() ,
,
![]() for which
for which
![]() is a minimum. For most practical
matrices this optimum value of the relaxation parameter can be found from numerical
experiments.
is a minimum. For most practical
matrices this optimum value of the relaxation parameter can be found from numerical
experiments.