1 Introduction

We have seen that discretisation of PDE's leads naturally to a matrix equation for a vector of unknowns which might represent nodal values of a function, local averages of a function or coefficients in an expanion in terms of a set of basis functions which generate an approximation space. In most real problems the dimension of the coefficient matrix is so large that Gauss elimination is not a feasible option, so that an interative method must be used to approximate the solution vector. We take as our model problem

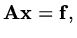$${\rm\bf A}{\rm\bf x}={\rm\bf f},$$ (129)

where 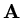${\rm\bf A}$ is a `non-singular 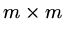$m\times m$ matrix. For any 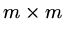$m\times m$ matrix 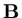${\rm\bf B}$ we can write

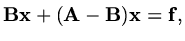$${\rm\bf B}{\rm\bf x}+({\rm\bf A}-{\rm\bf B}){\rm\bf x}={\rm\bf f},$$ (130)

so that

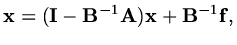$${\rm\bf x}=({\rm\bf I}-{\rm\bf B}^{-1}{\rm\bf A}){\rm\bf x}+{\rm\bf B}^{-1}{\rm\bf f},$$ (131)

and we can seek an iterative solution by the algorithm ${\rm\bf x}^{(0)}={\rm\bf0}$,

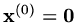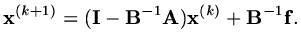$${\rm\bf x}^{(k+1)}=({\rm\bf I}-{\rm\bf B}^{-1}{\rm\bf A}){\rm\bf x}^{(k)}+{\rm\bf B}^{-1}{\rm\bf f}.$$ (132)

We will use the notation

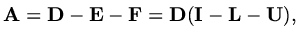$${\rm\bf A}={\rm\bf D}-{\rm\bf E}-{\rm\bf F}={\rm\bf D}({\rm\bf I}-{\rm\bf L}-{\rm\bf U}),$$ (133)

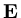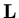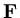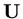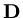where ${\rm\bf E}$, ${\rm\bf L}$ are strict lower triangular matrices and ${\rm\bf F}$, ${\rm\bf U}$ are strict upper triangular matrices and ${\rm\bf D}$ is a diagonal matrix.