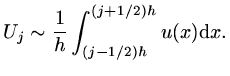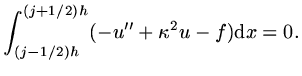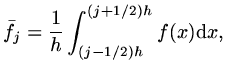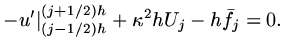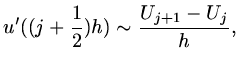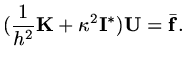Next: 3 Finite Element Method
Up: 1 Model Problem
Previous: 1 Finite Differences
Contents
It has already been observed thay many differential equations which we owuld like to solve
come from conservation laws which are integrals over volumes. This idea has been carried onto the discretisation
of such equations by instead of interpreting 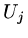 as an approximation to a point value,
as an approximation to a point value,
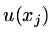 , rather
, rather
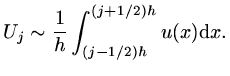 |
(49) |
In one sense we now reverse the process by which we arrived at the differential equation
from a conservation law: take the differential equation and integrate
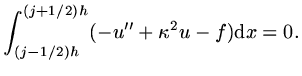 |
(50) |
If we integrate the first term and define
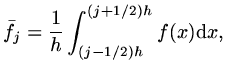 |
(51) |
then
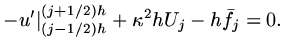 |
(52) |
Alternately we can think of applying a conservation argument to the `volume'
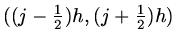 .
The difficulty now is to represent the `fluxes' across the faces of the volume at
.
The difficulty now is to represent the `fluxes' across the faces of the volume at
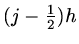 ,
,
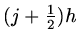 in terms of the integral quantities,
in terms of the integral quantities, 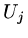 .
In this simple case we approximate
.
In this simple case we approximate
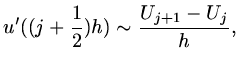 |
(53) |
so that we end up with a coefficient matrix which is identical to the finite difference
one we derived above, but the right hand side is now a vector of integrals of 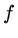 ,
,
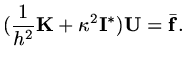 |
(54) |
While this appears very similar to an ordinary finite difference method, if using
unstructured meshes in two and three space dimensions (so that the `volumes'
are either arbitrary triangles or quadrilaterals) the finite volume method is much
easier to apply than conventional finite differences.




Next: 3 Finite Element Method
Up: 1 Model Problem
Previous: 1 Finite Differences
Contents
Last changed 2000-11-21
![]() as an approximation to a point value,
as an approximation to a point value,
![]() , rather
, rather